 |

 |
論説 |
 |
|
 |
 |
ICT活用による生徒の学習活動の変化と今後の教育
ー数学的活動の事例としてー |
|
| |
|
 |
| 1.はじめに |
教育でのコンピュータ活用が始まり,50年近くが経過し,21世紀に入り,ICT機器の進歩はますますスピードを上げている。eラーニングという言葉が使われるようになり,教育でのコンピュータの活用も大きく変化している。1950年代の終わりにアメリカで始まったCAI(Computer Assisted Instruction)が日本にも入り,1972年に一斉授業の中での個に応じた教育を目指し,CAIシステムが東京の公立中学校で動き出した。その後,現在のつくば市竹園東小学校のクラスルームCAIや金沢工業大学でKAPITALCAIが動き,コンピュータの利用範囲が拡大した。1985年には文部省(現在の文部科学省)が高度情報化社会に向けて義務教育段階からの学校教育へのパソコン導入の予算措置をとり,坂本昂が「マイコン教育元年」と述べ,教育でのコンピュータの導入が本格的に始まった。また,数学教育において,1990年にフランスでJean M.Labordeらによって開発されたMac版の図形の動的環境を実現したソフト(Dynamic Geometry Software:DGS)のCabri Geometry※注1を日本の授業で使うために中学校で使われているPC用に変換するとき,パソコンの機種間に互換性がなく非常に苦労をしたことは夢のようである。この数年の間に,学校と家庭でもICT環境が整備されたが,教育での活用はどのように進んでいるのであろうか。アメリカのテクノロジーを活用する数学教育の研究会Teacher Teaching with Technology
(T3)は,今年20周年を迎え,毎年約2000人の学校の先生や研究者が全米から集まり,4日間に200近いワークショップが行われ,グラフ電卓やコンピュータ活用の教材のいろいろなアイディアを出し,子どもたちのためにICTを取り入れた教育方法を研修し,議論している。日本でも,10年前にT3の日本支部ができ,今年で11回目を迎える。150名近い会員が実践事例を発表したり,ワークショップを実施している。活躍している人たちは10年前とあまり変わらない。限られた人たちだけがテクノロジーの利用を実践しているのは数学教育においてだけかもしれないが,高度情報化社会で生き,身近にある日常の便利な道具としてICTをいやおうなしに使いこなさなければならない子どもたちのために,ICTの活用を勧めている本誌の読者の皆さんと,教育を効果的に実施できるよう,ICT活用の効果を再確認し,より多くの分野で,多くの人に広めることを考えていきたい。
まず,ICTの活用で変わる生徒の思考過程や学習活動の変化について考察する。
|
|
|
 |
| 2.自ら発見する学習 |
コンピュータを使うことで,自ら発見し,知識を構成していく学習が可能になることが示されたのは,パパートが開発したLOGOが出てきたり,図形を動的に扱うDGSや簡単に表示されるグラフを視覚的に観察しながら関数を探究できる関数ソフトが開発されたりしてからである。LOGOは画面の上の亀(タートル)の形をしたカーソルを作図する手順に従って動かすことができるプログラム言語である。子どもたちが自分で作図手順を考え,プログラムし,その亀の動きを観察し,論理的に筋道を立てて考える場を作った。彼はこれをマイクロワールドと呼んでいる。その結果,学習者は,自分で図形についての知識を構成していくと考え,ここで子どもたちは自分の数学的思考を孵化していくことができるといっている(シーモア・パパート,1982)。
また,DGSの代表的なものとして,フランスで開発され,世界中の子どもたちが使っているCabri
Geometryや,日本で主に使われているGeometric
Constructor※注2がある。DGS環境では,子どもたちが自分で図形の性質や関係を発見していく。たとえば,中学校の図形の学習で2点を通る円の作図について学んだとき,生徒たちは,図1の左のように,円をたくさん描いて,右のように1つ1つの円を2点を通るように動かし,円の中心が2点の真ん中を通ることを自分で見つけることができた。次に,3点を通る円について考えたとき,生徒たちは,その円は1つしかないことや,その中心の性質を自分で見つけることができた。

▲図1 2点を通る円
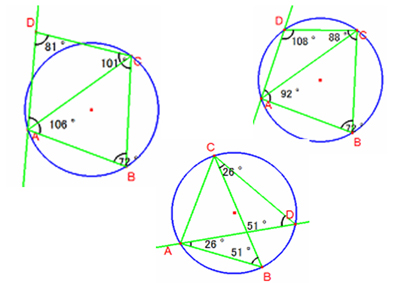
▲図2 4点を通る円
さらに,4点を通る円を考えたとき,生徒たちは,図2の点Dを円周上になるように動かし,4点が円周上にきたとき対角の和が180度になること,さらに,円周角が等しいことなど円に関するいろいろな性質を自分で見つけることができた。このように,円についての探究を2点から始まり,3点なら,4点ならと発展させていくことができる。図形の問題は分からないと絶対にやらなかった生徒が,コンピュータ室に来て,自分で見つけた中点連結定理を確めるために,まず三角形を描き,中点をとり,辺の長さや角の大きさを表示し,三角形をいろいろ動かして納得していた姿を思い出す。このように,図形を動かしながら,試行錯誤し自分で図形の性質を見つけ,知識を構成する活動が可能になると,子どもたちは積極的に授業に参加するようになる(清水克彦・垣花京子(1999))。図形を動的に扱える環境では,図形の証明に関して,生徒が苦手な演繹的な証明に対して,納得しながら進められる帰納的な証明活動をどこまで認めるかが研究者の間では議論されている。
次に,関数の学習についてみると,関数グラフソフトGrapes※注3を使い,いろいろな関数のパラメータを動かしながら,グラフを観察し,その特徴を理解することができる。たとえば,図3のように,2次関数もy=ax²+bx+cと入力し,パラメータa,b,cを自由に動かし,グラフの動きを観察しながら,それぞれの係数の特徴を見つけることができる。比例から入り,y=ax,y=ax²と細切れに教えられている関数を,よりアクティブに,総合的に見ることができ,生徒自身で系統化でき,いろいろな関数を体験できる。関数の指導でも,視覚的かつ動的に扱える環境を積極的に利用した新しい流れを考えていかなければならないだろう。

▲図3 パラメータを変化させた2次関数のグラフ
最近の教科書や本には視覚的に表現しようと図やグラフが多いが,図やグラフも静的なものでは必ずしも分かりやすくなるわけではない。本誌で,紙の上に描いてしまうと動的に扱っているその変化を表すことはむずかしい。テクノロジーを使うことで動的に図形やグラフを扱うことができ,きれいな図やグラフが描けるだけでなく,紙と鉛筆では同じ条件の図形や関数のグラフを2,3個の例を作るだけであるが,生徒が納得するまで見ることができ,図形や関数式の中にいつでも変わらない性質や規則的に変わる性質を見つけることができる。そして,子どもたちが自分で自分の知識を作っていく学習活動が生まれる。ここでも,教師が持っている知識を生徒に与えるだけの授業ではなく,生徒が自ら知識を作っていくことが可能になる。このように,コンピュータやグラフ電卓を使うことで,数学的学習活動は具体から抽象へ進み,一般化する活動が可能になり,証明活動に関しても帰納的な証明で納得し,演繹的な証明の必要性を実感させることができる。
|
|
|
 |
| 3.覚えるから探索・考える・判断する学習へ |
世界中,大人も子どもも携帯電話を持ち,日常的にいろいろな機能を使いこなしている。電話やメールと同時に,辞書や辞典代わりに使っている。

▲図4 等距離地点を求める問題
分からない漢字や言葉,英語が出てきたとき,携帯電話で調べ始める。どこかに出かけようとするときには経路や時間をインターネットで調べてから出かける人も多い。地図もどこでも簡単に見つかる。数学の公式も,何を使えばできそうかが分かれば,覚えておかなくても,インターネットで探せば出てくる。このように,人々はいろいろな場面でインターネットを使って情報を探し,選択し,利用している。
例えば,図4のような問題(Kakihana, K. 他,2000)を,短大の学生がコンピュータ室で行ったとき,まず,何人かの学生が表計算ソフトを利用して,1単位ごとの距離を入力し,グラフを見ながら問題解決をしていた。距離を求めるとき三平方の定理を使う必要が出てきた。すっかり忘れていた学生はすぐにインターネットで調べ始めた。分かりやすい説明や利用できない説明などいろいろな情報から,自分で理解できる情報を探し,式を見つけ,計算は表計算ソフトの機能を使って行っていた(図5)。

▲図5 表とグラフを使って問題解決
さらに,両地点から同距離の点を求める段階では,表計算ソフトで描かれたグラフの交点の周りの座標を細かくし,y軸の値が同じになる点を求めていた。今までは式を解くことができなければ解けなかった問題も,グラフを読みながら1つの解を得ることができた(図6)。
このような問題は,学生たちのほとんどはコンピュータ環境がなければ,手をつけることもできなかったであろうが,コンピュータを使うことで楽しみながら問題解決を行っていた。

▲図6 グラフから解を求める
正確に式を解いて答えを出すまでいたらなかった学生もいるが,今までは挑戦もしなかった問題に挑戦し,覚えていない公式もインターネットで調べることで思い出し,必要に応じて,その知識を使いながら,考え,判断している。計算式を解くことはできないが,近似値を求めることができる。このような問題解決のアプローチも,ICT時代では認められるのではないだろうか。そして,情報化社会を生きる子どもたちにとって,必要な知識を探し,適用し,問題解決をしていくことが重要になる。そこで,われわれは,ICT活用の教材を考えるとき,その場面で何が必要かを判断し,情報を探し,考えながら問題解決するようないろいろな場面を提供し,その問題解決のプロセスを体験できるようにしていく必要があるだろう。
|
|
|
 |
| 4.個に応じる教育の変化CAIとeラーニング |
中山和彦と東原義訓(1986)は,CAIのI(Instruction(教授))をL(Learning(学習))にかえ,CALとし,学習者の立場に立って,コンピュータが教えるのではなく,学習者の自発的な学習をコンピュータが支援するシステムへと発想を転換し,一斉授業の中で個に応じた教育の実現を目指した。
現在は,eラーニングと呼び,CAIとはいわないが,インターネットとコンピュータを使って個々の学習者を対象とし,自学自習を支援するものがある。たとえば,大学が提供しているeラーニングのコンテンツには,教員が説明する声を流しながら,パワーポイントで作られた画面を写したり,黒板に書かれている内容をカメラで写したりし,その授業を再現するものがある。学生が授業時間以外でも,どこでも,いつでも学べる環境を提供している。一般の人でも学ぶことができる。さらに,インターネットを通して,グループウェアを活用し,離れた人と議論をしたり,情報交換をしたり,学び合ったりする協働学習も盛んに行われている(余田義彦,2003)。
また,最近はインターネット上で授業用のWebページを作るためのフリーウェアもある。簡単に学習用のコンテンツを作ることができ,参加を許可された人たちによるコミュニティを作り,参加者の学習履歴を保存し,学習状況をチェックすることができる。
公開されている学習用コンテンツには,CAIが始まった初期のころに,コンピュータに人間教師の代わりをやらせていると非難されたことと同じではないかと考えてしまうものもある。しかし,今後は,多くのコンテンツが公開され,すべての人が学ぶ場が学校だけでなくなり,公開されているコンテンツを使いながら自学自習したり,自分にあったコミュニティに参加したりして学習するということが多くなるだろう。教室の中で行われた個に応じたCAIに対して,eラーニングは教室にとらわれず,どこでもいつでも学習者それぞれが自分の都合に合わせて学習できる環境になる。ますますその学習コンテンツの質が重要になる。そこで,eラーニングのコンテンツの質を上げ,効果的な学習を実施するために,コンテンツ作成に,中山ら(1986,ibid.)が実践して成果を挙げた学習者の立場に立った一斉学習の中で個に応じるコースウェアの開発の理念やノウハウを再び伝え,活かしていくことが必要であろう。
|
|
|
 |
| 5.最後に |
以上,数学教育を中心にICTを活用することで学習活動がどのように変わるかを述べてきた。1つは,コンピュータによる動的な環境の提供により,学習者は,具体的から抽象化,一般化へと数学的活動ができる。さらに,図形の扱いで見てきたように,2点から3点,4点を通る円へと1つの課題を発展させていくことができる。また,関数の探求でも,今までの方法では解くことができなかった問題を自分なりの方法で解決することができた。今回は説明しなかったが,グラフ電卓を使うことで,整数の並びや計算のしくみのいろいろな規則を見つけ,問題を発展させていくことも可能である。学習者は,ちょっとした知の創造の体験ができ,今までの学習範囲から大きくジャンプアウトできる。もう1つは,インターネットの普及により,eラーニング環境でいつでもどこでも学習ができるようになり,どんな知識もWebを通して簡単に得ることができる学習環境での学習活動である。そこで,問題解決に,使える公式や考えを覚えるより,探し,提供されている内容を比較し,判断し,利用できる能力が非常に重要になる。
40年前に大型計算機でシミュレーションしながら解決をしていた現実の問題をパソコンでシミュレーションすることもできる。調べたい知識はインターネットを通して簡単に調べることができ,その道の専門家が答えてくれる環境もある。さらに,携帯電話が単なるコミュニケーションの道具だけでなく,何らかの学習環境を作っていくと考えられる。今後,携帯電話と同じくらいの大きさのパソコンが手元にいつもあるようになるであろう。このような環境では,何を基礎基本の知識とするかを明確にし,大量な情報を選択・判断できる力,大量の数値データを整理・分析できる力を育てていくことが重要である。
今までは教科を中心に,学習指導要領に従って,その学習内容の中でICTの活用がどのように可能かを追求し,それらの効果を示してきた。しかし,ICTを使うと可能になる新しい学習内容や活動も出てくる。ICTが社会を変え,学習環境を変えている以上,今後の教育では,新しい時代に対応できる,今までとは違う新しい内容やアプローチを組み込んだ学習活動を考慮したものを求めていきたい。
|
|
|
 |
注1:Cabri Geometryは現在,Cabri Logo社の製品としてCabri Geometry II Plus, Cabri 3Dとして発展し販売されている。これら
のソフトで作図した図をオブジェクトとして,ホームページやMicrosoft Wordにのせ,図形を操作することもできる。
注2:Geometric Constructor(通称GC)は愛知教育大学の飯島康之氏
(http://www.auemath.aichi-edu.ac.jp/teacher/iijima/iijima.htm)が開発し,フリーでダウンロードできる作図ツールである。インターネットからも教材をダウロードしたり,作図を追加 できる。
注3:Grapesは大阪の高校教員の友田氏が開発したフリーの関数グラフソフトで,いろいろな関数の探求ができる。
http://okumedia.cc.osaka-kyoiku.ac.jp/?tomodak/grapes/
<参考文献>
・シーモア・パパート(1982),マインドストーム,奥村貴世子訳,未来社
・清水克彦(1998),コンピュータ教材と子どもの学び,佐伯胖他編集,「情報とメディア」,岩波書店
・清水克彦・垣花京子(1999),コンピュ−タで支援する生徒の活動(シリ−ズ/課題学習・選択教科としての数学授業に使えるソフト)
数学科・図形分野での新しい展開,明示図書
・中山和彦,東原義則(1986),末来の教室,筑波出版会
・中山和彦,木村捨雄,東原義則(1987),コンピュータ支援の教育システム−CAI,東京書籍
・余田義彦編著(2003) ネットワークで育む「確かな学力」つくば市共同学習プロジェクトへの挑戦,21世紀教育研究所
・Kakihana, K., Fukuda, C. & Shimizu, K.(2000) The Effect of Integrated Learning of Functions Using Computers^ As
Quantitative Literacy in a Two-Year College Program^,ATCM2000,
・NAEP(1998),NAEP in mathematics for 12th glade.
|
|
|
|
 |
 |
 |